Apparently someone thought it was too hard to actually measure the heat going into the gas in the Heat Capacity Ratio measurement.
They were right about the hard part. It is a very difficult measurement to make.
Anyway, rather than fix the terminology and theory that made the experiment appear to make no sense, particularly the part about it actually yielding a very useful result...
So they just rewrote the experiment so its easy to do.
Its also easy to get any number you want as an answer, from 1 to infinity. See chapter Basics if you want the gruesome details.
So, we have demonstrated no need to fix known broken terminology and theory. But we can change the experiment to make it easer to run, even if it no longer gives us the same answer or a repeatable answer or a useful answer.
(To be fair, there is a more reliable and simple way to calculate the Gamma constant for a gas. No one actually uses the above method, or someone would have noticed it does not work.)
|
Even Quainter, after all these years!
Now in good old 2012, we got around to fixing that little puzzle about gases having two specific heats, right? Nope. Instead we changed it so you can get literally any number you want from it.
Example: from the site that rhymes with encyclopedia*. :
The heat capacity ratio or adiabatic index or ratio of specific heats, is the ratio of the heat capacity at constant pressure (Cp) to heat capacity at constant volume (Cv). It is sometimes also known as the isentropic expansion factor and is denoted by γ (gamma) or κ (kappa). The latter symbol kappa is primarily used by chemical engineers. Mechanical engineers use the Roman letter. (Still total nonsense).
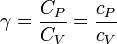 where, C is the heat capacity and the specific heat capacity (heat capacity per unit mass) of a gas. Suffix P and V refer to constant pressure and constant volume conditions respectively.
To understand this relation, consider the following experiment:
annnd Here is the rest, so you know. You just can't make this stuff up....
A closed cylinder with a locked piston contains air. The pressure inside is equal to the outside air pressure. This cylinder is heated to a certain target temperature. Since the piston cannot move, the volume is constant, while temperature and pressure rise. When the target temperature is reached, the heating is stopped. The piston is now freed and moves outwards, expanding without exchange of heat (adiabatic expansion). Doing this work cools the air inside the cylinder to below the target temperature. To return to the target temperature (still with a free piston), the air must be heated. This extra heat amounts to about 40% more than the previous amount added. In this example, the amount of heat added with a locked piston is proportional to Cv, whereas the total amount of heat added is proportional to Cp. Therefore, the heat capacity ratio in this example is 1.4.
(Notice the smoke and mirrors near 40%, actual measurements and arithmetic are left out? If this was a way to calculate Gamma, That would mean
Pressure = Gamma*Volume, not
Pressure = Volume Gamma. You cannot measure the total amount of heat added by this method, the adiabatic expansion follows a different work path. It matters how you get from A to B on a Pressure x Volume Graph, if you are calculating work, which is area under a curve.)
And it looks like this (everywhere):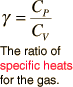 
The γ in "γ = ..." is called gamma.
|
