Simple steam recycling model demonstrates the 'Carnot Limit' fallacy.

   Previous Next

Even a naive look at steam heat recycling does NOT support the "temperature ratio" limit.
(This is also known as the "Carnot Limit", which is unsupported by Carnot's actual publication. It would be a disservice not to acknowledge that.)

  • Below are "Carnot Limits" ranging from 32% to 46%, and computed efficiency from 56% to 98%. So clearly an exception to the "rule".
  • Universal limits of the universe really should not have exceptions.
  • Temperatures are not meaningfully comparable from inside to outside a heat engine.
  • Temperatures are not proportional to energy between different substances.
  • Temperature is not proportional to energy in the same substance between different solid, liquid or gas phases.
  • Pressure is approximately proportional to energy.
  • Pressure is meaningfully comparable between inside and outside of a heat engine.

Three cases of steam

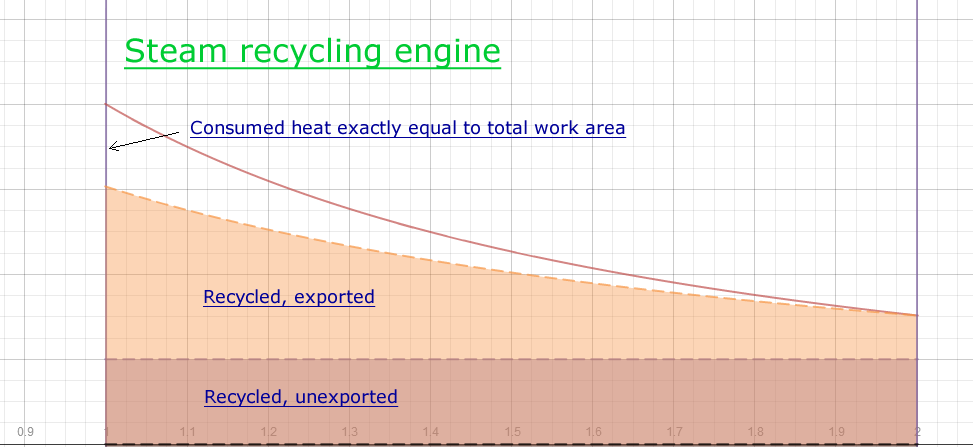
Case 1, Steam recycling low pressure

  • pressure +3 atmospheres 4 total
  • Temperature 132° C 405° K
  • Clapeyron/Carnot Ratio ~77%
    (expansion factor of 2)
  • Temperature Ratio
    (aka misnomer Carnot Limit)
    1-300/447=32%
  • Total work area ~(.23/.4)*4=2.3
  • Work against pressure envelope, 1
  • Efficiency (2.3-1)/2.3 = 56%

Graphs

Steam limits

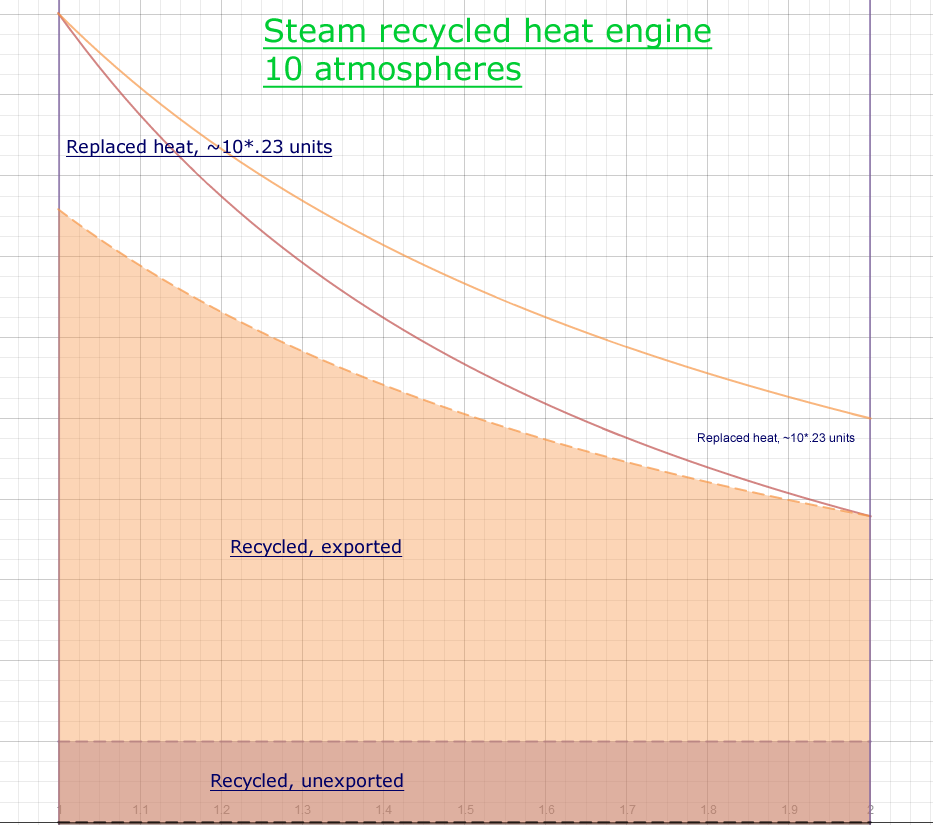
Case 2, Steam recycling medium pressure

  • pressure +9 atmospheres, 10 total
  • Temperature 174° C 447° K
  • Clapeyron/Carnot Ratio ~77% (expansion factor of 2)
  • Temperature Ratio
    (aka misnomer Carnot Limit)
    1-300/447=32%
  • Total work area ~(.23/.4)*10=5.75
  • Work against pressure envelope, 1
  • Efficiency (5.75-1)/5.75= 83%

steam recycle 10 bar

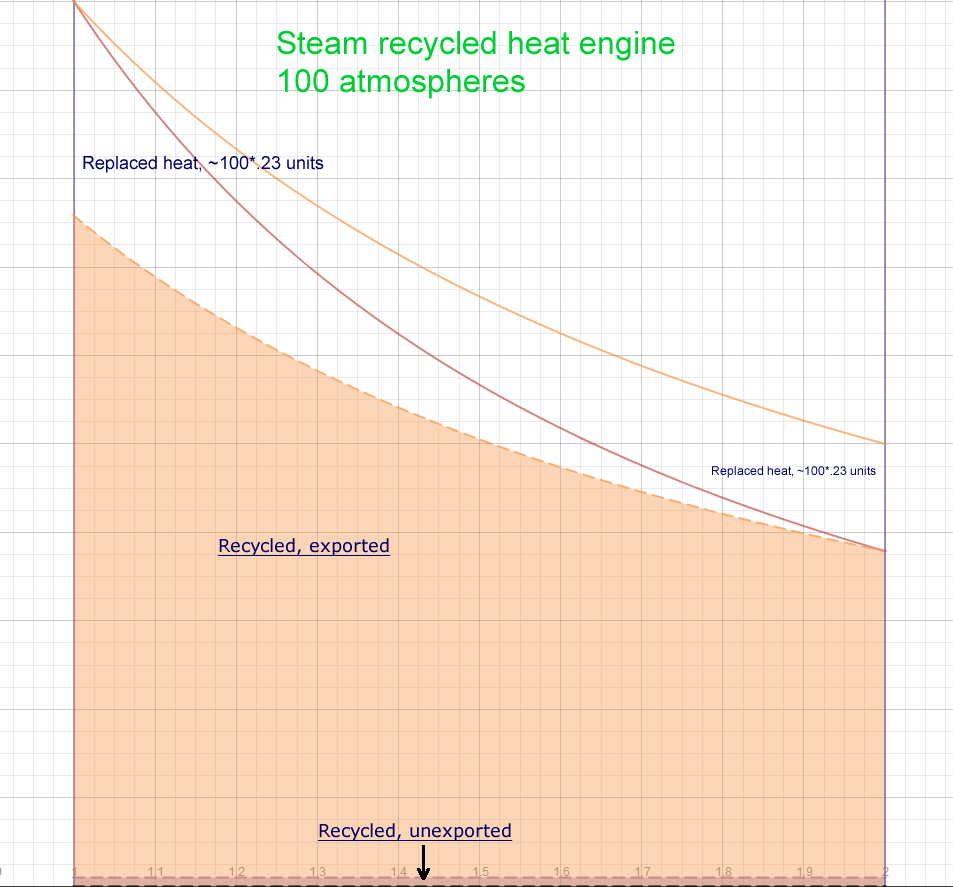
Case 3, Steam recycling High pressure

  • Pressure +99 atmospheres 100 total
  • Temperature 286° C, 559° K
  • Clapeyron/Carnot Ratio ~77%
    (expansion factor of 2)
  • Temperature Ratio
    (aka misnomer Carnot Limit)
    1-300/559=46%
  • Total work area ~(.23/.4)*100=57.5
  • Work against pressure envelope, 1
  • Efficiency (57.5-1)/57.5= 98%

steam recycle 100 bar