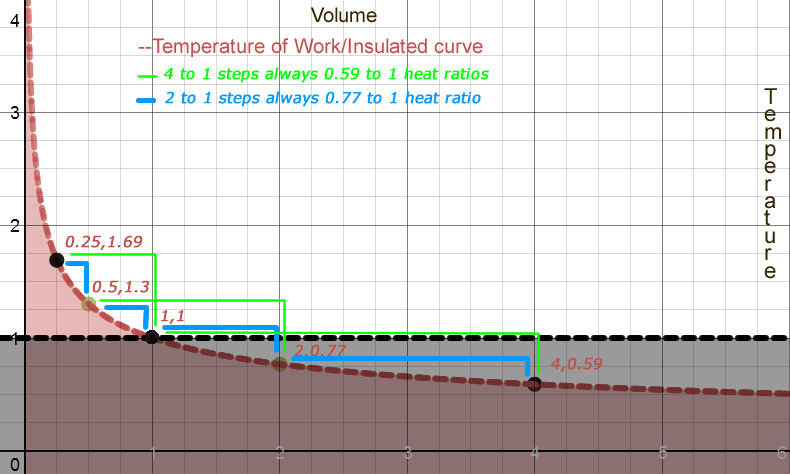
Pick any two points the same multiple apart, the same ratios appear
The Heat Ratio is the ratio of heat before and after a Volume change of a given multiple apart. Take any volume V as the starting point. Double that volume. For air, the relative heat is a factor of 0.77 smaller.
H(2*V) = 0.77 *H(V)
If its H(4 * V), the constant is 0.59, or 0.77 2
That is just a mathematical property of an exponential curve.
The Work Ratio = 1 - Heat Ratio.
It is also always the same for given multiples of Volume.
Work(2*Volume) = (1-0.77)*Heat(Volume)
...
= 0.23*Heat(Volume)
The Work Ratio is calculated on the assumption that all the energy in the system is heat, at volume V. Work is the portion of Heat converted to work as insulated volume increases. It nears 100% only for very large multiples >1000.
The Pressure Envelope prevents a productive expansion beyond the Envelope's pressure. This is one source of the misconception that some fundamental conversion limit exists.
|
The Heat Ratio and the Work Ratio (AKA Carnot Ratio) are Relative to any starting point.
The expansion is only productive until the constrained volume pressure equalizes with pressure envelope. If one calculates fuel efficiency by heat conversion alone, a false economy appears with hyper extended volumes. (Such as Atkinson cycle engines). Heat is genuinely consumed, work is done in equal measure, but a portion of the work is uselessly fighting atmospheric pressure.
|

