Hot Air expands, pushes something, Ta-da! Work!
When air is compressed, work is added to it by the container compressing it. When Air expands, work is subtracted- transferred to the container that is expanding.
There is a particular curve related to this, called the adiabatic curve in most texts.
Adiabatic comes from a Greek root meaning "armored", "impassable" or "impervious". Lotta help there. Of course its impassable, its compressing and expanding air. If it was passable the air would leak out.
Adiabatic means the Pressure curve that happens when the air chamber is Insulated against heat transfer. So no energy is getting in or out, except the mechanical work of compression and expansion.
This work corresponds to an exact amount of heat energy. If you add the heat some other way, like fire, you still get the same amount of work when you expand the gas.
How hot does it get? Well it depends on the gas, density, and so on. What does NOT depend on the gas, is that an equal amount of energy is converted to heat for an equal amount of work, or volume change times pressure. And the reverse is true, an equal amount of work can be produced from an equal amount of heat. Reversibility.
If you get 1 unit of heat from compression at pressure X, you can get 1 unit of work from expansion at the same pressure. And heat from work is the same as heat from chemical reactions or solar power. All interchangeable.
Same goes for adding and subtracting heat. The amount of heat energy which must be added to go from temperature A to temperature B, is the same amount as must be removed when going from temperature B to temperature A. |
Work Transfer Curve
AKA Work Curve
AKA Adiabatic Curve
AKA the Insulated Curve
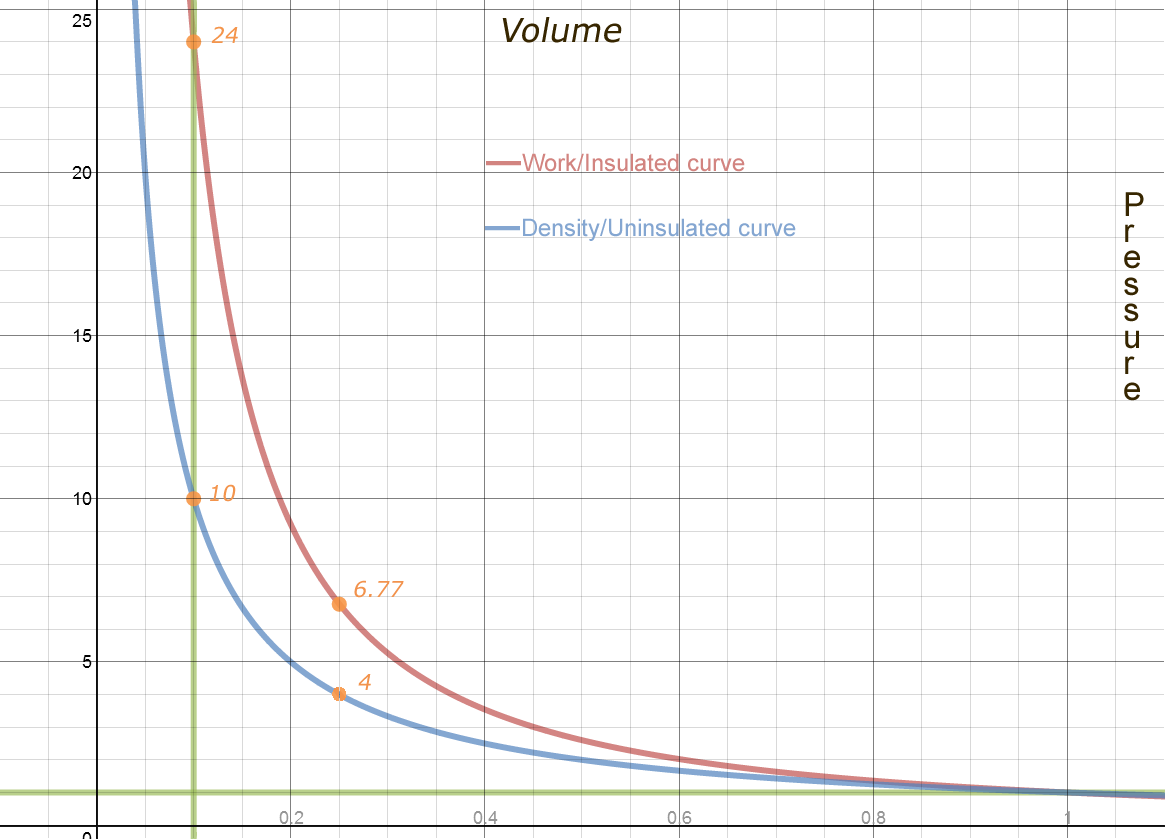
Above is the Work Transfer Curve or Work Curve. Adiabatic is misleading, as it means no heat is added or subtracted. But you are adding heat when you compress. Removing heat when you expand. No "other" heat is added or subtracted such as by by diffusion or heating. "Insulated" is a more accurate term.
The important thing, is that moving left and right on the volume scale, stores or releases work energy inside the working vapor (air, steam or other gas-phase matter). That's the key to heat engines. Perfect equivalence of energy as either heat or mechanical work as volume increases and decreases. Perfect transformation from heat to or from work, in either direction.
Above, the red curve is the Adiabatic, or Work Curve. It is the Insulated case, the pressure when no heat is allowed to diffuse into or out of the vapor chamber as volume changes. The Blue Curve is the Isothermal or Density Curve. It is the UN-insulated case, the pressure that results from increase in density at the same temperature. Also the curve you get if you let all the added heat escape as the vapor is compressed.
The above graph assumes both curves started at the same place, a pressure and volume of 1. If instead of compressing, we expanded from there, the Insulated case would cool, and its pressure fall below the UN-insulated case. Heat will flow from ambient surrounding air into the UN-insulated case, to replace the heat lost due to the work of expansion.
The blue curve's pressure is inversely related to volume, y=1/x or x-1. Or pressure = 1/volume = volume -1 .
Multiply the blue curve by the relative heat to get the red curve. If Ambient heat is 1, then when the volume is less than 1, the relative heat is greater than 1.
The actual formula for pressure of the work curve, is x-k, where k is a number greater than one. Pressure = Volume-k
The exact number for air, isn't exact at all. You can find references for the adiabatic compression for air to 1 tenth volume ( 10 to 1), as being 22 atmospheres or 25 atmospheres or somewhere in between. The exact constant depends on composition, such as humidity. The constant for steam is completely different, and yet in a similar range. The constant is always more than 1, because 1 is the exponent for the change in density due to change in volume. K will be 1 (the relative density vs volume) + the ratio of heat capacity of gas to work required to expand to the same volume and pressure (for air, about .4) or 1.4 total for air.
To get the precise number for the air you are using, you can compress the air by a known factor, 10 times, 4 times, just known. Measure the actual pressure.
The constant is Ln(actual pressure)/Ln(compression factor). Above, at the top orange point, at x=1/10, the calculation is Ln(24)/Ln(10) or about 1.38. We can also calculate the same constant anywhere along the curve, for example, the Orange dot at x=1/4 yields Ln(6.77)/Ln(4). Still 1.38.
And strange but wonderful, the constant does not matter in making heat engines, because for every constant, the work is given by Pressure times Volume change and for every constant, the same amount of heat is generated by that work. The temperature may be different for different vapors because the specific heat of different vapors differs.
The total heat energy stored is still exactly the same. You get back what you put in, exactly. If you add the heat from burning a CC of fuel, you get the same heat energy, the same average pressure, and the same work, for any vapor. So use any vapor that's handy to make your engine. Some exotic rare gas won't behave significantly any differently than the vapor we walk around in that we call air.
The constant is also often rounded to 1 digit, 1.4 not 1.41. Why? Because the actual value of the constant is canceled out. Energy in = Energy out, whatever the constant. Its precise value is unknown, as the composition of air is somewhat variable. But the precise value does not affect the outcome. So just remember - Whatever the constant, Energy in = Energy Out every time, or it’s wrong.
|

