Gamma is the exponent of the Work Transfer Curve

   Previous Next

Symbols often used are γ (gamma) or κ (kappa). The value is a constant based on the specific heat of the gas (which is also a constant).

What they are not...

Your physics texts show it is the result of calculating a ratio of Specific heats of a gas with constant pressure to constant volume. (and blah blah... this bit varies) Total nonsense.

Example: from the site that rhymes with encyclopedia*. :
The heat capacity ratio or adiabatic index or ratio of specific heats, is the ratio of the heat capacity at constant pressure (Cp) to heat capacity at constant volume (Cv). It is sometimes also known as the isentropic expansion factor and is denoted by γ (gamma) or κ (kappa). The latter symbol kappa is primarily used by chemical engineers. Mechanical engineers use the Roman letter. (Still total nonsense).
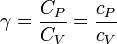Heat Capacity ratio Formulawhere, C is the heat capacity and the specific heat capacity (heat capacity per unit mass) of a gas. Suffix P and V refer to constant pressure and constant volume conditions respectively. To understand this relation, consider the following experiment:

annnd Here is the rest, so you know. You just can't make this stuff up....
A closed cylinder with a locked piston contains air. The pressure inside is equal to the outside air pressure. This cylinder is heated to a certain target temperature. Since the piston cannot move, the volume is constant, while temperature and pressure rise. When the target temperature is reached, the heating is stopped. The piston is now freed and moves outwards, expanding without exchange of heat (adiabatic expansion). Doing this work cools the air inside the cylinder to below the target temperature. To return to the target temperature (still with a free piston), the air must be heated. This extra heat amounts to about 40% more than the previous amount added. In this example, the amount of heat added with a locked piston is proportional to Cv, whereas the total amount of heat added is proportional to Cp. Therefore, the heat capacity ratio in this example is 1.4.
(Notice the Notice the smoke and mirrors near 40%, actual measurements and arithmetic are left out? If this was a way to calculate Gamma, That would mean Pressure = Gamma*Volume, not Pressure = Volume Gamma. You cannot measure the total amount of heat added by this method, the adiabatic expansion follows a different work path. It matters how you get from A to B on a Pressure x Volume Graph.)

And it looks like this (everywhere): 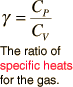  Heat Capacity ratio Nonsense
The γ in "γ = ..." is called gamma.
(The above paragraph is from anther site. They probably would not want credit. You can find it in lots of Physics texts too.)

Heat Capacity Ratio Debunked

Basically, all the various ways of getting (Cp) and (Cv) presume they somehow embody the work it took to get there. If you follow the Work pressure curve for expansion, that's sort of true for one of them. The other point - you could get there with an isothermal (uninsulated) expansion, a silly sine wave, a constant pressure expansion or an infinite number of other ways. All having different amounts of heat energy added or work done.

Now look at the green X points, very far apart. The red X points, very close together. Not the same ratio. This formula will not yield a constant, it yields a function of Volume.

The science of specific heat is wrong.
If (Cp) and (Cv) are specific heat of a particular vapor, they are equal at all volumes and temperatures and pressures for which the vapor exists. So (Cp) / (Cv) = 1, always, according to the ideal gas law.
The premise is wrong.
Charitably assume the real point is to compare two amounts of heat by comparing two points on a volume pressure graph. Still, the ratio of the two points depends on the Volume. The ratio varies from 1 to infinity as Volume goes from one to infinity. So you can use this method to calculate any number between one and infinity, if you pick the right volume. A universal random calculator, you have a 1/infinity chance of choosing the right value of V. Any point you pick also doesn't uniquely define the work or heat it took to get there.
Isobaric Expansion is a red herring.
(Well it would have been useful if anyone had measured the heat it took to get there, but as written here, its useless.)
The only reason this is remotely useful is that by coincidence it ends up at the same temperature as the other curve (a Work Transfer Curve) began at. So one can determine the Temperature ratio, and hence the Heat Ratio and Work Ratio. None of these are Gamma. One can compute Bk, the constant formerly known as (Gamma-1), from the Heat ratio, if you also know the precise Volume expansion done and can take a logarithm.
The math is wrong.
Pressure = Volumeγ. So γ ( gamma) is an exponent. To calculate an exponent from numbers on curves, you need to throw a logarithm in there someplace. The ratios of an exponential curve with every other curve constantly changes. If you could just take the ratio of a couple points or numbers to calculate exponents, mathematicians wasted a lot of time figuring out how to take logarithms.
Speed of Sound is irrelevant.
γ  (gamma) may have a place in calculating the speed of sound, but that is totally irrelevant to discussing transformation of work to/from heat via Pressure times Volume change. It lends credibility to the common misconception that to get compression heating, compression must be done quickly. (Wrong!).
The spelling is ok.
Not actually sure about this, I'm a terrible speller. Trying to say something nice. The Font's were Jim Dandy too.

*Sites that rhyme with Encyclopedia are amazingly accurate and perform an amazing service for dissemination of knowledge. They can only be as accurate as the state of the art, and the accepted state of the arts is what our Universities Teach. The misinformation above can be found in any physics text book used by any University in America in 2012.

γ (gamma) or κ (kappa) are the negative exponent of Volume to calculate the Insulated Pressure Curve, aka Work Transfer Curve, aka Adiabatic Curve

You can calculate it like this. Compress your vapor a factor of 10 in an insulated container.
γ = Ln(actual pressure)/Ln(10)
Whew, that was a difficult one. You can choose any number besides 10 you like, except 1. Even expand instead of compress (that would be a fraction between 0 and 1). Can't use 1 because that's no volume change You must change the volume to calculate the exponent.
γ = Ln(actual pressure)/Ln(volume compression factor)

Texts give a value of 1.4 for double atom gases like air, and 1.7 or 1.66 for single atom gases like helium. They also give 24 (or 22 or 25) as a frequent pressure (in Atmospheres) for a 10 to 1 compression of air. Which disagrees slightly with 1.4. This is a function of specific heat of a gas, which vary even within types of molecules.

Now, if Air compressed by a factor of 10 is at 24 atmospheres of pressure, Ln(24)/Ln(10) = 1.38, not 1.4.
If air is at 25 atmospheres, Ln(25)/Ln(10) is 1.4. Does it really matter if its 1.4 or 1.7 to make a Heat Engine? Nope. Click Next to see why.

The Work formula from Gamma is W = (VFinal1-γ - VInitial1-γ)/(1-γ) which is confusing, because its not obvious (1-γ) is negative. γ is the exponent of the Work pressure curve. So to get actual work, which is pressure times volume change, integrate the Work pressure curve or ∫ V-γ= V1-γ/(1-γ). Why? Because Integral of X to the N is ∫ XN is XN+1/(N+1), even if N is Negative. Because its a negative exponent it is simpler to write (1-N) than ((-N)+1)

A few Pages Back, we showed the Heat Curve, which is H = V1-γ. Also, the Work Pressure Curve = Relative Density Curve * Relative Heat Curve or = V-1 * V-(γ-1).

Since Heat Engines are about Energy Heat and Work, we note the relative density curve is unhelpful, and that we can directly calculate Work from The Heat curve, rather than from integrating the Pressure Curve. So by defining a new Energy Exponent constant Bk = γ-1, then
Heat = K*Temperature
Temperature = Volume-Bk
Bk*Work = Temperature
Bk*Work = Volume-Bk
Bk*Work = VInitial-Bk - VFinal-Bk
and
Work = (VInitial-Bk - VFinal-Bk)/Bk
Bk Air ~= 0.4 or 0.4
Bk Single Atom molecules~= 0.66 or 0.7

Its important to keep in mind these are relations on the relative scale, where initial values of Temperature, Heat, Pressure, Volume are all set to 1. So Bk*Work=Temperature is on the relative scale, not Absolute. On an Absolute scale, using the same units of Energy for Heat and Work, Consumed Heat = Produced Work and vice versa.

Note Bk*Work is Bk * Pressure * Volume is an Area. To Calculate this area requires Bk to already be known.

If Bk is defined γ-1, observe the dominant property determining γ's value is simply the geometric relationship between Volume and Density, and the property of a gas is secondary. The value of Bk is uniquely a property of a gas, not geometry. It isolates the physical property unique to each vapor's specific heat.

(Why Bk for the constant? Bekause its easier to find on my keyboard than Greek letters, Bekause Beta is one less than Gamma, all the single letter constants are taken, and just Bekause.)

What's the deal with Molecules and γ (or Bk)?
(This is for fun, Hard scientists, please skip.)

The Atom science guys will roll in their graves, but it seems easier to comprehend things we can visualize.

Imagine Atoms as weightless, frictionless, perfectly bouncy beach balls. Add a grain of sand at the center for weight.

Now to interact with these, they can bounce. That's it. If they spin, or if the grain of sand spins, the outside world can't interact with that. That is a single atom gas, like Helium.

Now tie a couple Beach Balls together. That's a double atom gas, like Oxygen or Nitrogen. Now they can bounce as they move in a straight line as a pair, or they can spin in place, and bounce off something it spins into. So Two ways to store energy with the same mass. Even if the speeds are the same, the beach balls spinning at Speed S have as much energy as when they go in a straight line at Speed S.

Average Speed at the tiny scale is roughly the same as temperature at the large scale. Put in the same amount of energy to Single or Double Beach balls, the Single beach balls are going faster. The Double Beach Balls are doing combinations of moving in a line and spinning, and are going slower at each, on average, but the total amount of movement is the same in both systems.

When Bk ~= .7, it means the Temperature for a given amount of total Heat energy is higher, because the single atoms are averaging a faster speed. When Bk ~= .4, the Temperature is lower than for .7, but still higher than it started. The average speeds are slower, total energy the same, and total motion is a sum of spinning and linear motions.