How they calculated Gamma in the early 1800's (from Specific Heat)?

   Previous Next

So if our formula for Heat Capacity Ratio is different, were they that confused in early 1800's?
Or are we confused 200 years later?

The math

Ok, it is part happy accident the 1800's method works, but mostly they did incredibly accurate measurements, and then observed.

First quick summary. Area on a Pressure x Volume graph is Work. The Beta constant, Bk is 1 less than Gamma. The Work Pressure Curve is Volume-1 x Volume-Bk or V-1-Bk. Integral of Xn is X1+n/(1+n). To get the area under the Pressure Curve (which is work), Area = Work = V1-1-Bk/(1-1-Bk) = V-Bk/(-Bk). If you start at Volume 1 and end at Volume Final, this simplifies to -(V:final-Bk-1)/Bk or (1-V:final-Bk)/Bk which ought to look familiar-ish. Graphed, the Y axis is Pressure, the X axis is Volume. Also, V:final-Bk is relative heat or temperature, so this will simplify further to (1-RelativetemperatureFinal)/Bk or (1-TempFinal/TempInitial)/Bk. Which really ought to look a lot like the Work Ratio seen elsewhere.

Now for some specific heat. (Cv) the specific heat under constant volume, is the only specific heat a gas has. Cp "means" the "Specific Heat under Constant Pressure", is a misnomer. Under constant pressure means the volume is allowed to increase, and is balanced by an exterior pressure. Actually, Cp = Cv + (The heat converted to work). How much work? The constant Pressure times (VolumeFinal - VolumeInitial) or just Pressure times Delta Volume. (difference not ratio). The "curve" in this instance is a flat line at Pressure. The area under the curve is a rectangle, easy to figure. So the work portion is the same for all gases. How much heat? The exact same amount of energy as the work.

So recall Gamma = Cp/Cv,
Gamma simplifies to Gamma = Cv/Cv + (work energy)/Cv
or 1 + (Work Energy)/Cv.
and recall specific heat is heat (or energy) per degree
gamma = 1 + (Work Energy)/(Heat Energy/1 Degree)
or
gamma = 1 + (Work Energy)*(1 Degree)/(Heat Energy)

Work Energy per unit area is 1. Heat Energy per degree is specific heat, Degree per Heat Energy is 1/specific heat.

So the happy accident is Cv/Cv = 1, which is what needs to be added to Bk to get Gamma.

From above, Work = Area = Work Heat/Bk. Solve for Bk...
Bk = Work Heat/Area,
where Work Heat is the heat consumed to produce a given amount of work (Area) and Area is the rectangular volume under the constant pressure line.

Also, "heat" is relative to the total heat per unit volume. Unitless. Heat can be considered as ranging from 0 to 1. Every unit increase of volume places the SAME amount of energy in that volume and consumes the SAME amount of work (and heat) to expand.

Who is confused? Year 1800 or year 2012. Unfortunately, 2012

Bottom Line, because the integration of the pressure curve puts The exponent in a position of a coefficient, and because measuring BOTH the specific heat and the work heat gives the information to calculate the coefficient, the 1800's Heat Capacity Ratio method works. The 2012 method yields any number between 1 and infinity, depending.

The 2012 Heat Capacity Ratio method isn't "Fixable" because it does not include actually measuring the heat that went into the work. Unless you already know the exponent, it isn't fixable.

Why the change? Consider how hard it is to measure accurately the amount of heat which you put into a volume of air. Must have multi digit precision on the amount of heat a flame or electric wire emits, must know the specific heat of the container, so it can be subtracted, very difficult in 2012. How much more difficult in 1810? But they did it, accurately, 200 years ago.

So somewhere along the line, someone who didn't understand the 1800's method added a shortcut, which was just wrong.

Final Note

"Heat Capacity Ratio" is historically used to represent Bk+1, or Gamma. However, Bk is literally the gases capacity to store heat relative to the amount of work at any point on a Pressure Volume graph. Neither the heat capacity nor the amount of work are constant, but the ratio is constant. Both capacity and work are multiplied by Pressure or Volume. If Bk = .7, then the heat stored in the gas can do the work of about 1/.7 or 1.3 ish volume-pressure unit squares. If its .4 (air), it can do the work of 1/.4 or 2.5 squares. A unit square is always the same amount of work, if on the same scale. The actual constant best fitting the definition, which is a simple function of specific heat, is Bk, not Gamma.

The 1800's scientists were amazing.

TABLE OF THE SPECIFIC HEAT OF GASES.

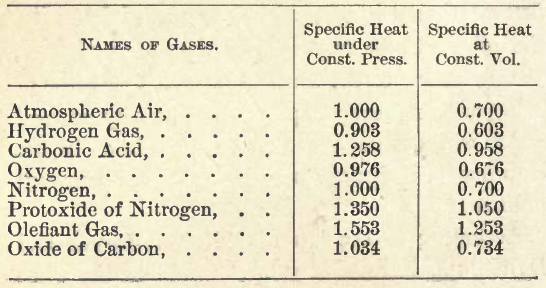
Specific heat table

Table from "Reflections" page 76, Sadi Carnot.

Sadi Carnot recognizes that the difference is a constant, the same for all gases. So not a property of a gases specific heat.

Page 76
The difference between specific heat under 
constant pressure and specific heat under constant
volume is the same for all gases.

-and pg 77-
The first column is the result of the direct
experiments of MM. Delaroche and Berard on the
specific heat of the gas under atmospheric pressure,
and the second column is composed of the numbers
of the first diminished by 0.300.

For the table above one would get:

  • Atmospheric air, Bk =.300/.700 = .42
  • Carbonic Acid, Bk =.300/.958 = .31
  • Oxygen, Bk = .300/.676 = .44
  • Nitrogen, Bk = .300/.700 = .42
  • Protoxide of Nitrogen, Bk = .300/1.050 = .28
  • Olefiant Gas, Bk = .300/1.258 = .24
  • Oxide of Carbon = .300/.734 = .41
  • (Helium, not listed, would be about .300/~.450 ~ .7)

Ok, correction is still outstanding. Specific heat under constant pressure is a misnomer. The correct formulation would be:

Bk = (Work Heat Consumed)/(Cv).

Gamma = 1+Bk.

And Cp is a misnomer, and is equal to:
Cp = Cv + (The heat converted to work)

So they didn't get it precisely right, but the 1800 error is of terminology, not correctness of the result nor error in their method.