Kelvin's assertions stated as Theorems.

   Previous Next

Kelvin built on top of Carnot's sometimes imperfect foundation.

Commentary

The mathematics of the proof are in depth. Kelvin does not have the benefit of knowing the shape of the Work Transfer Curve is Volume to the exponent "-Gamma".

A simpler integration of Volume-Gamma yields the same answer.

However, several things are worth noting. The graph is a MUCH clearer example of the Carnot Cycle than the modern "Pressure vs Volume" graphs, as it make clear when temperature (and hence total vapor heat energy) are and are not changing. Oddly, the fact that temperature is NOT changing is evidence of heat being added or subtracted.

One mistake in the analysis, is that the same amount of heat energy is always delivered by a temperature "source" of a given temperature In fact, the heat added is a function of the length of the isothermal expansion. So the Temperature alone cannot predict the amount of heat added. What "fixes" this, is that the incorrect assumption is cancelled out by the fact that all 4 points, A, A1, A2 and A3 are fixed by two facts: 1) The temperatures high and low, and 2) the total volume change is always the same, and the intermediate volumes are selected to make the corners "touch".

 

Kelvin's other Theorems

Theorem K1: The amount of work produced by a heat engine is proportional to the amount of heat consumed in volume expansion of a vapor.

Proof: Is somewhat elaborate. Since it contains formulas not handled by the archive copy's character recognition. See "Reflections" pages 145, paragraph 16, through page 161, paragraph 28. Copying them here would be redundant and obscure this narrative rather than help it. His calculations are based on this graph which is a much simpler depiction of the Carnot Cycle than the usual Pressure vs Volume graph.
Carnot Cycle as temperature vs Volume

Proof is that Diffusion of heat is Waste.

This could be considered a corollary to Carnot's assertion about diffusion.

Insulated construction is the only known construction method for eliminating diffusion. May seem trivial, but as almost all Heat Engines 170 years later are still metal, apparently not obvious to everyone.

Theorem K2: Ideal Construction is Impermeable to Heat

Sadi Carnot did not describe construction of his cylinder, possibly he thought it was obvious. In any case, Lord Kelvin's spells it out. An Ideal construction is impermeable (insulated). 

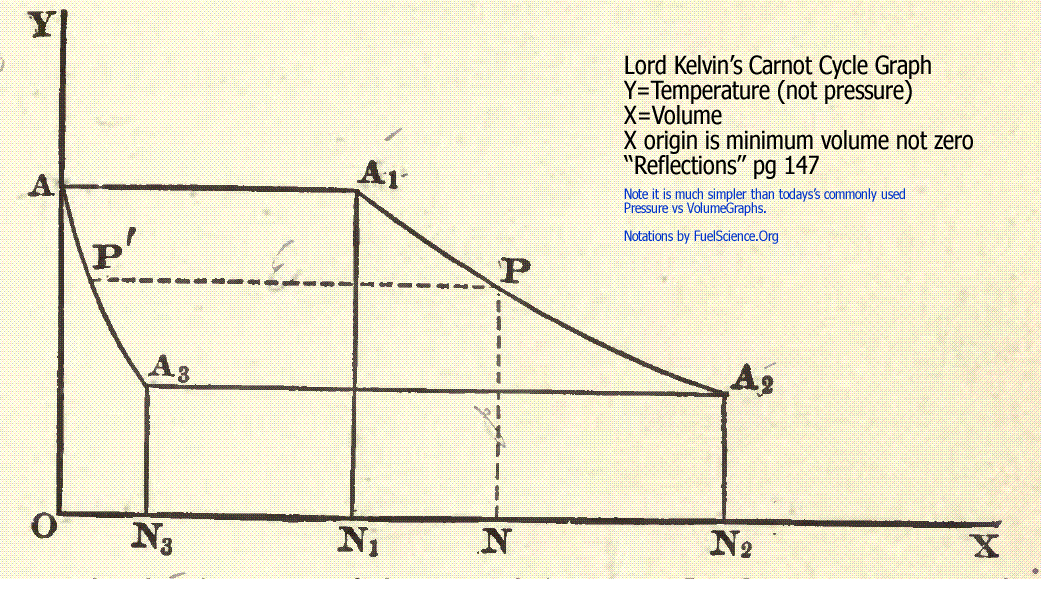
"Reflections" pg 141 (steam engines) by Lord Kelvin
paragraph 15. Let CDFE be a cylinder, of which the
curved surface is perfectly impermeable to heat,
with a piston also impermeable to heat, fitted in it ;
while the fixed bottom CD, itself with no capacity
for heat, is possessed of perfect conducting power.
Let K be an impermeable stand, such that when
the cylinder is placed upon it the contents below
the piston can neither gain nor lose heat.
 
pg 152 (Air engines) by Lord Kelvin
paragraph 22. In the ideal air-engine imagined by Carnot
four operations performed upon a mass of air or
gas enclosed in a closed vessel of variable volume
constitute a complete cycle, at the end of which
the medium is left in its primitive physical condition;
the construction being the same as that which 
was described above for the steam-engine, a body
A, permanently retained at the temperature 8, and
B at the temperature T\ an impermeable stand K\
and a cylinder and piston, which in this case contains
a mass of air at the temperature S, instead
of water in the liquid state, at the beginning and
end of a cycle of operations. The four successive
operations are conducted in the following manner :

However, he also compares it to the latent heat of Steam at various temperatures, apparently including the heat of vaporization, which is indeed part of the latent heat, but which is not recoverable as motion, as temperature drops to condensation point, expansion of vapor stops as its volume collapses to water. This phase change prevents this energy from being converted through volume expansion.

It can be shown that Work is directly proportional to Temperature change due to Volume Change. This is a simpler result than predicted, but still within Lord Kelvin's prediction.

Theorem K3: Work will be a computable function of Temperature

Kelvin postulates that the amount of Work done is calculable from the Temperature drop. It is again spread over many pages, so is not copied here. "Reflections" Page 163-168, Kelvin uses Greek symbol Mu ( μ ) As a function (or constant) that relates Temperature to Work. His explanation with regard to steam led to the conclusion that Work is a variable function of Temperature, but still a function.

Footnote:See previous page footnote regarding credits to Kelvin & Carnot. Above it is attempted to tie the specific lessons of their work to the text from which the lessons are derived.

Lord Kelvin's mathematical proof that Work or "Mechanical Effect" was done prior to and without the benefit of the establishment that Pressure is an negative exponential function of Volume. The calculations are done in the domain of Temperature vs Volume, and reach the same answer. He drew one conclusion that is incorrect, that any gas will behave the same and produce the same work for a given temperature drop. This is approximately but not precisely true. Monatomic gases have a lower specific heat, and so contain less energy for a given temperature drop. His conclusion that Work is proportional to the Heat energy is nevertheless sound, as is the implied conclusion that Work is proportional to temperature drop and applies to all gases. The constant of proportionality may vary from one gas to another.